结构方程模型介绍

结构方程模型分析(SEM)是一种能够把样本数据间复杂的**因果联系**用相应的模型方程表现出来并加以测量、进行分析的计量技术。结构方程模型针对一些数据本身不能直接询问或测量得到，即所谓以**潜变量**的形式，对数据模型进行估计的分析方法。

结构方程模型常用于验证性因子分析、高阶因子分析、路径及因果分析、多时段设计、单形模型及多组比较等。结构方程模型常用的分析软件有LISREL、Amos、EQS、MPlus。

## 01 模型组成

结构方程模型由三个基本变量、两个模型组成

![图片](/upload/turndown-pics/20231210/640_wx_fmt_png_wxfrom_5_wx_lazy_1_wx_co_10.png)

三种变量：

（1）观测变量，即**显变量**，是可以通过访谈或其他方式调查得到的，用长方形表示；比如图中的x1-x3，就是观测获取的变量。

（2）结构变量，是无法直接观察的变量，又称为**潜变量**，用椭圆形表示；如图中的F1-F3

（3）误差变量，观测变量无法完全解释结构变量，总会存在误差，这反映在结构方程模型中就是误差变量。用圆形表示；如图中的e1-e9

显变量和潜变量两者同时也具有以下两类特质，分别是内生变量和外生变量。**内生变量**是指模型内决定的变量，一般受外生变量影响，即效应变量或因变量，有内生显变量和内生潜变量。即在路径图中，有箭头指向它的变量。它们也指向其他变量。**外生变量**是指模型以外的其他因素决定的变量，即起因变量或自变量，有外生显变量和外生潜变量。在路径图中，只有指向其他变量的箭头，没有箭头指向它的变量均为外生变量。

结构方程模型分为两个重要部分，分别是测量模型和结构模型；**测量模型**是用作分析显变量与潜变量之间的关系；而**结构模型**是利用路径分析方法建立潜变量之间的关系，并对潜变量之间的关系加以分析。

![图片](/upload/turndown-pics/20231210/640_wx_fmt_png_wxfrom_5_wx_lazy_1_wx_co_11.png)

结构方程模型与路径分析主要区别就在于完整的结构方程模型包含了测量关系，如果仅包括影响关系，此时称作路径分析。

## 02 模型构建步骤

结构方程模型的建模步骤大致分为五步：

**1、模型构建**

在做结构方程模型的建模之前，应该充分意识出现的**各种变量间的各种关系**，确定潜变量和观测变量，潜变量和潜变量之间的关系。各个变量组合之间可能存在多种路径图，且都会有存在理论支撑的特定的含义，这时建议选择更简单的模型来解释更多的变量，用简单的模型表达更多的含义。

**2、模型识别**

模型识别就是判断引入数据后的结构方程模型能否运行及拟合成功。从数学上来讲，就是看列出的方程能否求解。识别结果包括三种，包括不可识别、恰好识别和过度识别。在结构方程模型中，如果包含p个观测变量，存在t个自由估计参数，自由估计参数与观测变量的数量关系，会有以下三种情况:

- 如果`t<p(p+1)/2`，假设的理论模型可能具有唯一解，但是因为方程式的数量多于估计参数数量，常常导致模型的过度识辨。

- 如果`t=p(p+1)/2`，假设的理论模型一定得到唯一解，这时模型与数据之间达到理想的适配程度，但是因为卡方值等于零，造成无法进行适配检验。

- 如果`t>p(p+1)/2`，因为方程式的数量少于估计参数数量，导致无法进行参数估计，模型无法识辨。

**3、模型拟合**

模型拟合就是将收集到的数据导入软件进行参数估计，先进行**验证性因子分子**，进行**测量模型**的估计与检验，再通过**路径分析**，进行**结构模型**的估计与检验。参数估计方法常用的为极大似然法(ML)、一般化最小平方法 (GLS）和未加权最小平方法(ULS)。

在观测变量是连续变量的情况下，如果样本数据为随机抽取，并符合多变量正态性分布，样本数量为中等规模或者较大规模，则可以选用ML方法或GLS方法。

当样本数量较少时，或者样本数据不符合多变量正态性分布时，也可以运用GLS方法。

如果选择运用ULS方法，并不需要一定符合某种统计分布，常常就可以得到达到检验标准、比较令人满意的估计结果。

在结构方程模型中，如果观测变量的数量较多，就会产生较多的参数估计，这时应该有较大的样本数量与之相对应。对于不同的参数估计方法，对应的**样本数量**的适应程度也不尽相同。通常情况下，运用ML方法时，样本数量往往在500 以上；运用GLS方法时，样本数量介于200-500，或者样本数量与变量数量之比介于10:1到15: 1，这时可以得到较好的参数估计效果 。

**4、模型评价**

模型评价是指结构方程模型建立后,判断输出结果的指标值是否符合模型预设的**适配度标准**。这一步需要检验模型的内在质量并且评估模型的整体适配度。本文采用的指标及适配标准如所示。

![图片](/upload/turndown-pics/20231210/640_wx_fmt_png_wxfrom_5_wx_lazy_1_wx_co_12.png)

**5、模型修正**

在模型拟合后，若拟合指数反应该模型拟合不良，则需要通过模型修正来调整。模型修正要慎重，需要根据拟合指数来增加、删除变量，调整路径或参数，使得拟合度达到最优，主要在进行增删调整等操作时需有一定的理论支撑。同时理论的结果还要与实际的意义相连接来反映修正模型的过程是否得当,反复调整最终得到理论和实际均适合的模型。

**修正方法**主要是增加或减少模型中自由参数的设定。对于通不过检验的参数可以固定参数值为0或1，通过减少自由参数个数来修正。对于模型拟合度低的情况，可以采取增加自由参数的方法。修正后再进行拟合，直到各个指标值都达到预设的标准。

---

### 相关参数概念简介：

1.潜变量：人为创造的无法直接被测量的变量，如研究气候（Climate）对微生物群落的影响，“气候”是个人为创造的抽象概念，没有一个准确的标准用于衡量这个指标。

2.显变量：也称观测变量，显变量的主要含义就是：变量是实际测量的内容，也就是各类型环境因子的数值。例如：通过温度、湿度、pH、光照强度等测量指标来作为气候的观测变量。

3.复合变量：这是一类区别于潜变量的特殊变量，简单来说就是若干个观测变量进行组合，作为原始变量，一般以六边形表示。如：将经度和纬度这两个观测变量进行组合，作为空间（Spatial）的组合变量，进行路径分析。

4.拟合度：也叫适合度、配合度，是结构方程模型中最重要的指标。拟合度指标是假设的理论模型与实际数据的一致性程度，模型拟合度越高，代表理论模型与实际数据的吻合程度越高。常见拟合度指卡方值、近似均方根误差等。通过这一系列拟合度指标判断设计的模型是否合理，能够较完整地解释原始数据矩阵间的关联。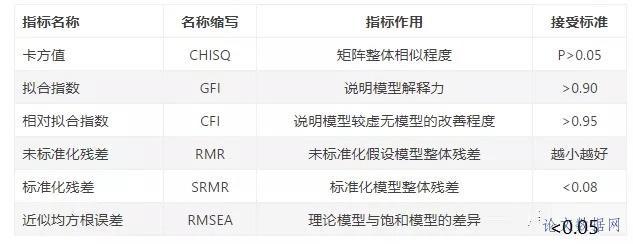

![](http://qiniu.papersdata.cn/FjOng-zXI1gSPJzfOsXuRruJu_hv.jpg!watermark)

5.标准路径系数：路径系数概念等同于回归分析中的回归系数，用于说明模型当中元素关系，回归系数>0则说明两个元素呈正向关联，值越大则说明关联程度越强。除路径系数外一般还会给出路径系数检验的P值用于判断该路径系数是否显著，还会针对每个元素给出回归分析的R2值，来说明元素整体被其他元素的解释程度。

2023-12-10 10:46 by admin 99 0

结构方程模型介绍

热门文章