首页
博客
理论工具
数据分析
spss分析
amos分析
python数据分析
结构方程模型
回归与中介
论文写作
未分类
数据服务
关于我们
0
个人中心
我的订单
退出
登录
登录
注册
Get Started
一元线性回归分析
[回归分析](regression analysis )是研究一个变量如何随另一个或一些变量变化的方法。例如,学习成绩会受努力的时间,方法,个人的智慧,教育资源等因素影响;疾病的发生与生活环境,方式,遗传因素,自身体质等影响。常见的回归分析有线性回归、非线性回归、多重线性回归、Logistic回归、Probit回归分析等等。本节主要讲解简单线性回归,即研究变量Y随变量X变化的分析,不考虑多个自变量对结果变量的情况。 线性回归(linear [regression] )是分析两个定量变量间的线性关系。一般地,某一变量(称为Y变量)随另一变量(X变量)变化而变化,且这种变化趋势呈直线趋势。 **线性回归模型的适用条件** 简称(LINE)(1)**线性**(linear) 因变量y与自变量x呈线性关系,通过绘制散点图,大致判断是否满足线性关系。 (2)**独立性**(independence) 每个个体观察值之间相互独立,即任意两个观察值之间不应该有关联。 (3)**正态分布**(normal distribution) 因变量y服从正态分布。即在一定范围内,任意给定X值,其对应的随机变量Y均服从正态分布。一般可以通过残差的散点图来判断;如果不满足正态性,可采用数据变换的方式使其满足正态性。 (4)**方差齐性**(equal variance) 在一定范围内,不同的X值所对应的随机变量Y的方差相等。通过残差图判断是否等方差性。 **回归分析的应用** (Ⅰ)描述变量间的依存关系 (Ⅱ)利用回归方程进行预测 (Ⅲ)利用回归方程进行统计控制 线性相关与回归的区别及联系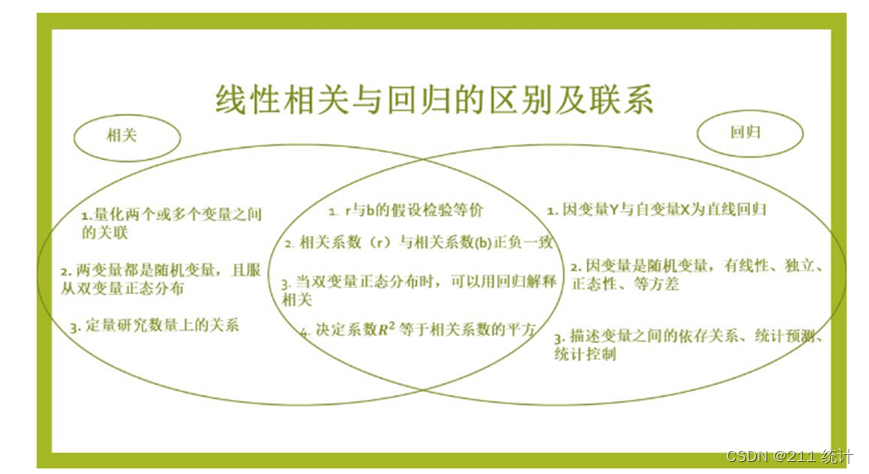 最小二乘法原则 通俗地讲, 通过样本数据(X、Y)的散点图,尽可能地让所有的散点与某条直线的距离“最近”
2024-07-27 17:25 by admin
70
0
注:本文转载自https://blog.csdn.net/2301_79384104/article/details/132306650,如有侵权行为,请联系我们,我们会及时删除。
热门文章
1
clashX 设置白名单,忽略本地hosts测试域名的代理设置。
2
验证性因子分析步骤以及应达到的标准
3
Spss详细图文教程——问卷信度和效度检验步骤图解
4
信度效度分析的注意事项
5
MATLAB时代的七种开源替代方案