中介效应-检验程序

## 检验程序

文献中存在多种中介效应检验的程序(MacKinnon, 2008; MacKinnon et al.,2002; 温忠麟等, 2012)，下面以最简单的中介模型为例说明中介效应分析的思路。如上图1，自变量X作用于因变量Y，路径系数c。由于不涉及第三个变量，所以c代表自变量作用于因变量的总效应。

一般情况下，只有当c显著或X与Y相关显著时才会考虑中介变量(e.g., Baron & Kenny, 1986; Judd & Kenny, 1981; 温忠麟等, 2012)，但不必然如此。上图是个单中介模型，a代表自变量X作用于中介变量M的效应，b表示中介变量M作用于因变量Y的效应，c’代表考虑或控制中介变量M后，自变量X作用于因变量Y的效应。

使用流行的统计分析软件或结构方程软件可以方便的获取a，b，c和c’的估计值及对应标准误，进行显著性检验和构建路径系数的置信区间(MacKinnon, 2008; Preacher & Hayes, 2008)。**总效应等于所有中介效应加上c = ab + c’。c为总效应，c’为考虑中介效应后的直接效应，ab为中介效应也称间接效应。**在回归模型中，ab = c-c’，但在其他模型（如logistic回归和多水平分析）中两者不一定完全相等(MacKinnon, 2008; 温忠麟等, 2012)。

### 3.1 逐步检验法

Kenny及其同事描述的中介效应检验程序是使用较多的检验程序，该方法易于理解和操作，具体步骤如下：

1.  检验总效应系数是否c显著，即自变量与因变量之间是否存在显著关系。如果c显著则继续进行随后的分析，如果不显著中介分析终止。
2.  检验自变量作用于中介变量效应a是否显著；如果a显著则继续进行随后检验，否则终止分析，中介效应不存在；
3.  检验中介变量作用于因变量效应是否b显著；如果b显著则继续进行随后检验，否则终止分析，中介效应不存在；
4.  检验直接效应c’是否显著。在a和b都显著的情况下，如果c’不显著说明存在完全中介(Judd & Kenny, 1981)，否则存在部分中介效应(Baron &Kenny, 1986)。

尽管逐步检验法易于理解和操作而且使用最频繁，但其存在问题也很明显。如前所述，c是否显著并非中介检验的必要前提，因为在有些情况下尽管c不显著仍然存在实质的中介效应即所谓的抑制模型(Suppression model)。如果按照逐步检验法的要求，c必须首先显著，否则中介变量无从谈起，而实际中c不显著而存在实质性中介效应的情况又非常普遍，所以**逐步检验法会错过很多实际存在的中介效应**。

### 3.2 系数乘积检验 -Sobel检验-

系数乘积检验就是检验ab乘积是否显著即H0：ab = 0，此程序常使用Sobel(1982)提出的标准误计算公式，因此也将此检验称作Sobel检验。

ab乘积是中介效应的大小，所以检验ab乘积是否显著是对中介效应的直接检验。ab乘积作为抽样分布，文献中存在多种计算其标准误的方法，其中最常用的是Sobel(1982)给出的公式：

$$ Sab\=b2Sa2+a2Sb2S\_{ab}=\\sqrt{{b^2} S\_a^2 + {a^2} S\_b^2}S\_{ab}=\\sqrt{{b^2} S\_a^2 + {a^2} S\_b^2} $$

$$ Sa2S\_a^2S\_a^2,Sb2S\_b^2S\_b^2 $$ 分别为系数a、b标准误的平方。系数乘积检验法的统计量是 $$ Z\=abSabZ=\\frac {ab}{S\_{ab}}Z=\\frac {ab}{S\_{ab}} $$，如果检验显著说明中介效应显著。此公式被常用的SEM分析软件采用，例如EQS，LISREL和Mplus。也有其他的分析程序(Preacher & Hayes, 2004)使用不同的标准误公式如：

$$ Sab\=b2Sa2+a2Sb2+Sa2Sb2S\_{ab}=\\sqrt{{b^2} S\_a^2 + {a^2} S\_b^2 + S\_a^2S\_b^2}S\_{ab}=\\sqrt{{b^2} S\_a^2 + {a^2} S\_b^2 + S\_a^2S\_b^2} $$

根据 SabS\_{ab}S\_{ab}可以构建中介效应的置信区间：

95% CI\=ab+1.96Sab95\\%\\ CI = ab + 1.96 S\_{ab} 95\\%\\ CI = ab + 1.96 S\_{ab}

系数乘积检验法存在的主要问题是，检验统计量依据的正态分布前提很难满足，特别是样本量较少时。因为即使a，b分别服从正态分布，ab的乘积也可能与正态分布存在较大差异。

### 3.3 差异系数检验

差异系数检验即检验H0：c–c’=0。通常情况下ab = c–c’，因此差异系数同系数乘积法有很多相同之处。c–c’的标准误估计通常使用如下公式(McGuigan & Langholz, 1988)。

Sc−c′\=Sc2+Sc′2−2rSc2Sc′2S\_{c-c'}=\\sqrt{S\_c^2 + S\_{c'}^2 - 2rS\_c^2S\_{c'}^2}S\_{c-c'}=\\sqrt{S\_c^2 + S\_{c'}^2 - 2rS\_c^2S\_{c'}^2}

ScS\_cS\_c和 Sc′S\_{c'}S\_{c'} 分别为两个直接效应估计的标准误， rrr 为自变量与中介变量的相关系数。差异系数采用 ttt 检验，其统计量为

t\=c−c′Sc−c′t = \\frac {c-c'}{S\_{c-{c'}}}t = \\frac {c-c'}{S\_{c-{c'}}} 。

模拟研究发现(MacKinnon et al., 2002)，系数乘积法和差异系数法比逐步检验法精确且具有较高的统计效力。

### 3.4 Bootstrapping

Bootstrapping的**原理是当正态分布假设不成立时，经验抽样分布可以作为实际整体分布用于参数估计。**

Bootstrapping以研究样本作为抽样总体，**采用放回取样，从研究样本中反复抽取一定数量的样本**（例如，抽取5000次），通过平均每次抽样得到的参数作为最后的估计结果(Efron & Tibshirani, 1993; Mooney & Duval, 1993)。

Bootstrapping不需要分布假设所以避免了系数乘积检验违反分布假设的问题，而且该方法不依赖标准误所以避免了不同标准误公式产生结果不一致的问题。模拟研究发现，**与其他中介效应检验方法相比Bootstrapping具有较高的统计效力。**因此，Bootstrapping法是目前比较理想的中介效应检验法(Preacher, & Myers, 2011)。

## 四、检验步骤

温忠麟与叶宝娟（2014a）提出了提出了一个较新的中介效应检验流程，见图2：

第一步，对总效应c进行检验，如果显著，按中介效应立论，否则按遮掩效应立论。但无论是否显著，都进行后续检验。

第二步，对中介效应所涉及的两个路径系数a和b进行依次检验，如果两个都显著，则间接效应显著，转到第四步；如果至少有一个不显著，进行第三步。

第三步，用Bootstrap法直接检验H0 : ab = 0。如果显著，则间接效应显著，进行第四步；否则间接效应不显著，停止分析。

第四步，确定中介效应存在后，检验直接效应c’，如果不显著，即直接效应不显著，说明只有中介效应。如果显著，即直接效应显著，进行第五步。

第五步，比较ab和c的符号，如果同号，属于部分中介效应，报告中介效应占总效应的比例ab/c。如果异号，属于遮掩效应，报告间接效应与直接效应的比例的绝对值|ab/c|。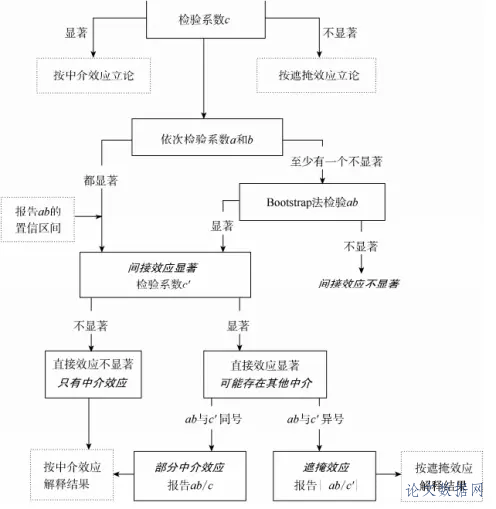

![检验步骤](http://qiniu.papersdata.cn/FqwkfLExmzVPkKZ5B3iS7s29Q4x1.png!watermark)

五、Stata 程序
----------

具体检验步骤如下：

### 1.逐步法

①**quietly reg** _Y X Controls_

②**quietly reg** _M x Controls_

③**quietly reg** _Y M X Controls_

### 2.sobel检验法

Sobel法是检验系数乘积法，其检验力高于依次检验，但这个检验统计量的推导需要假设a的估计\*b的估计服从正态分布,具有局限性。其代码如下：

**sgmediation** Y, **mv(**M**) iv(**X**) cv(**Controls**)**

> Y为被解释变量，mv( )括号里为中介变量，iv( )括号里为解释变量，cv（ ）括号里为控制变量。

**如何看sobel检验结果：**看Goodman-1(Aroian)那一行的p值，如果`p值<0.05`，则中介效应存在。如果中介效应存在，那么具体的直接效应值（direct effect）、间接效应值(indirect effect)和总效应值(total effect)可以看下面那个表的Coef.值。

### 3.bootstrap检验法（直接检验系数乘积的显著性）

Bootstrap法是一种从样本中重复取样的方法, 前提条件是样本能够代表总体(当然这也是通常取样进行统计推论的要求)。检验力高于Sobel检验。代码如下：

**bootstrap r(ind\_eff) r(dir\_eff), reps(500) : sgmediation** Y, **mv(**M**) iv(**X**) cv(**Controls**)**

estat bootstrap, percentile bc

同上，Y为被解释变量，mv( )括号里为中介变量，iv( )括号里为解释变量，cv（ ）括号里为控制变量。reps(500) 表示重复抽样500次。

#### bootstrap检验法如何看结果：

**不是看P值，是看\[BootLLCl , BootULCl\]这个置信区间，如果这个区间包含0，则不显著，如果不包含0，则中介效应显著。

**注：所有变量需要标准化处理。**

2024-08-05 10:55 by admin 35 0

注：本文转载自https://zhuanlan.zhihu.com/p/639200278，如有侵权行为，请联系我们，我们会及时删除。

中介效应-检验程序

热门文章