多重线性回归假设条件-残差正态性

**1.什么是残差？**

**残差即因变量的观测值Yi与利用回归模型求出的预测值^ Y之间的差值**，反映了利用回归模型进行预测引起的误差。

**2.怎么测量残差是否符合正态性？**

**例子**：分析住院费用与医院级别、地区、患者年龄、住院天数等的关系。

**数据展示**：

![](/upload/turndown-pics/20240811/v2-457d2191548eea5cced97882ef6dfbad_b0.jpg)

通过P-P图可以检验数据是否符合指定的分布。当数据符合指定分布时，P-P图中各点近似呈一条直线。

**Step1：**因为多重线性回归要求因变量符合正态分布，因此先利用直方图检验因变量“住院总费用”是否服从正态分布，结果如下：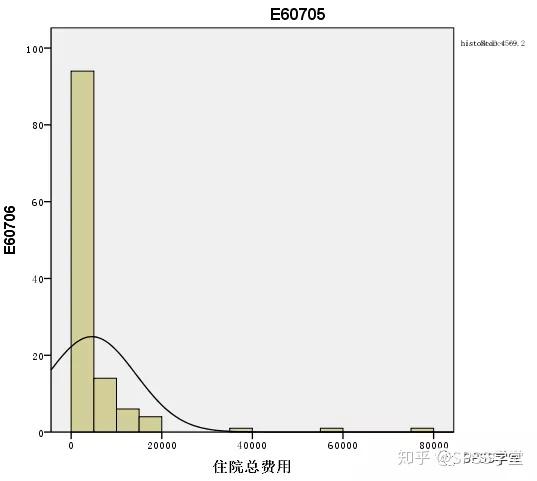

![](/upload/turndown-pics/20240811/v2-28324d236de9c8d41327976e0f9c49ae_b1.jpg)

**结果：**住院总费用不服从正态分布，需进行数据转换，可使用对数转换。在【转换】→【计算变量】中对“住院总费用”进行对数转换，新变量命名为“stan”。再重新绘制直方图，如下：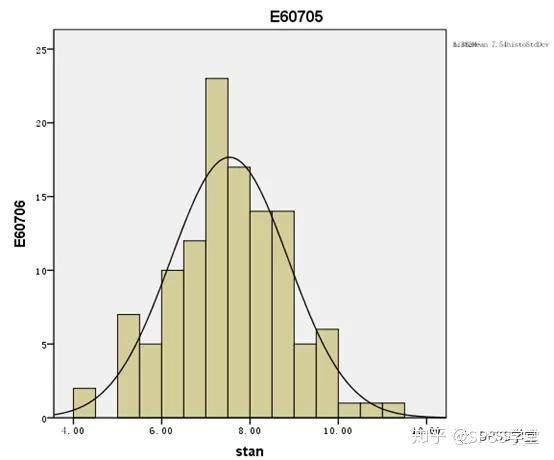

![](/upload/turndown-pics/20240811/v2-6b1157a83a013acac08cafaa73a517ef_b2.jpg)

**结果：**经过转换后，因变量符合正态分布。

**方法一 标准化残差直方图&正态概率图（PP图）**

**Step1：【**分析】→【回归】→【线性】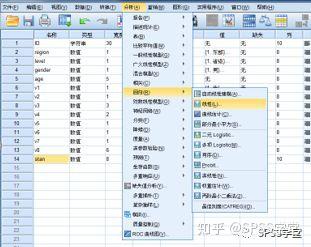

![](/upload/turndown-pics/20240811/v2-4007944ff6d8f04dfe9d2dbe4cf3fa21_b3.jpg)

![](/upload/turndown-pics/20240811/v2-4007944ff6d8f04dfe9d2dbe4cf3fa21_720w4.webp)

**Step2：**将“stan”移入“因变量”中，地区等变量移入“自变量”中。【绘图】→勾选“直方图”和“正态概率图”→“继续”。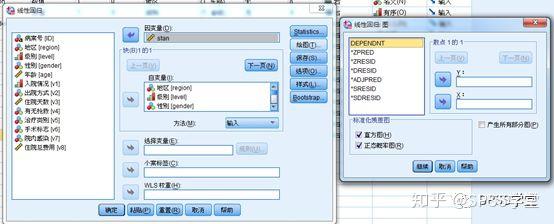

![](/upload/turndown-pics/20240811/v2-3929dc62eb9b7f9a70e78cbe1976d3db_b5.jpg)

**Step3：【**保存】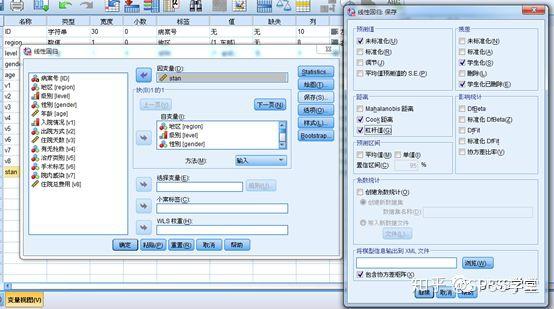

![](/upload/turndown-pics/20240811/v2-8993782bba7d97c3db5aee04433daf8a_b6.jpg)

**Step4**：结果输出与解读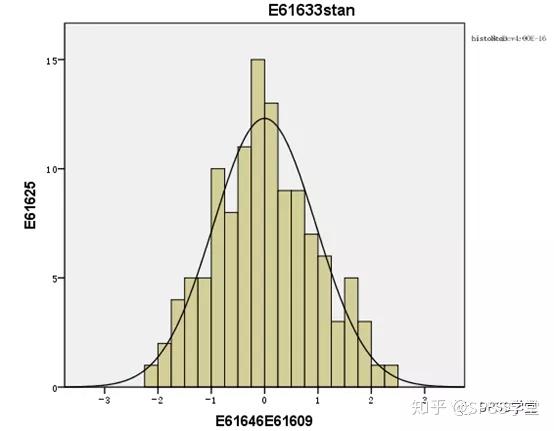

![](/upload/turndown-pics/20240811/v2-8ff70ef72c9efa32f58556d9d776531f_b7.jpg)

**结果：**标准化残差的直方图，符合正态分布。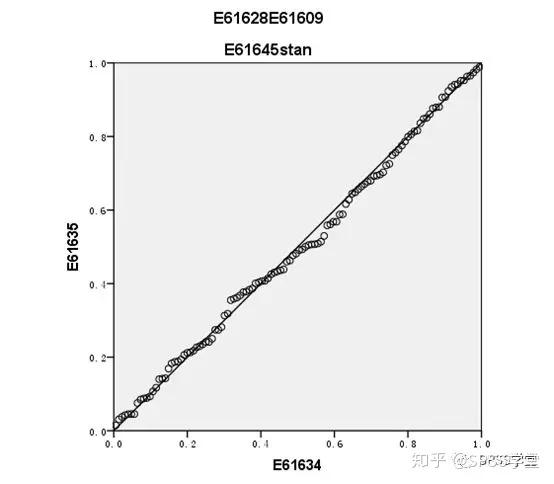

![](/upload/turndown-pics/20240811/v2-feda8a8e1c88d1afafa39953402dcf85_b8.jpg)

**结果：**标准化残差的正态概率图（P-P图），近似一条直线，符合正态分布。

**方法二 学生化残差绘制正态QQ图**

**Step1：【**分析】→【描述统计】→【Q-Q图】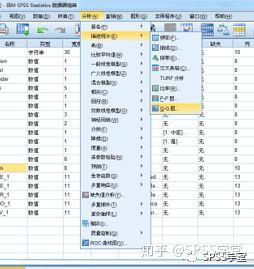

![](/upload/turndown-pics/20240811/v2-e2f0444fb36485887b30e46f3b1b0c03_b9.jpg)

**Step2**：将学生化残差SRE\_1选入“变量”（注：SRE\_1在上面的步骤中通过“保存”选项卡计算出来。）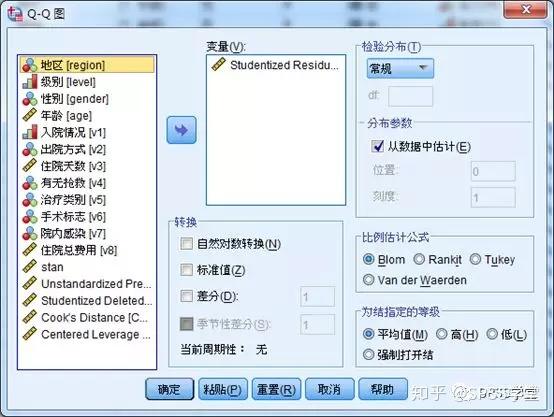

![](/upload/turndown-pics/20240811/v2-b8eb8dfe8d8480c97fb822a2a7bc7f0a_b10.jpg)

**Step3**：结果输出与解读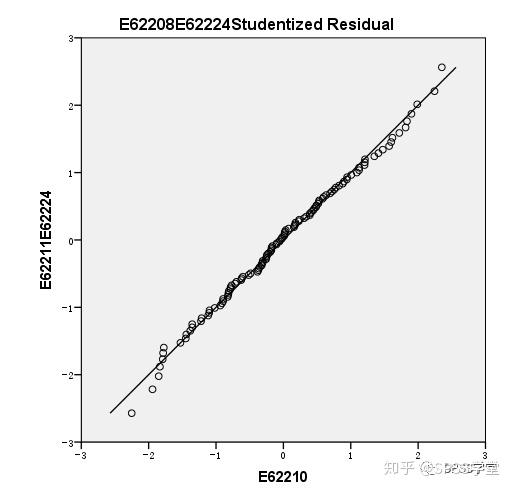

![](/upload/turndown-pics/20240811/v2-659d37f2a42bec72235298127fca4735_b11.jpg)

**结果：**所有点近似一条直线，学生化残差符合正态性。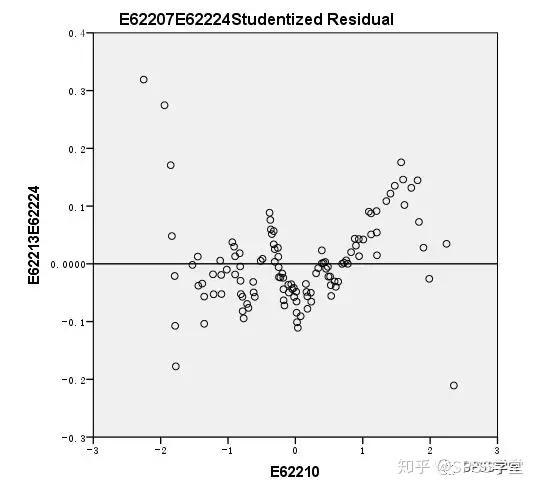

![](/upload/turndown-pics/20240811/v2-5912bc01d8efbd23c99021e7da9910f7_b12.jpg)

**结果：**所有点基本均匀分布于两侧，呈正态性。

**3.P-P和Q-Q图**

P-P图是根据**变量的累积比例**与指定分布的累积比例之间的关系所绘制的图形。通过P-P图可以检验数据是否符合指定的分布。当数据符合指定分布时，P-P图中各点近似呈一条直线。

Q-Q图由**标准正态分布的分位数为横坐标、样本值为纵坐标**的散点图。利用QQ图可鉴别样本数据是否近似于正态分布，若QQ图上的点近似地在一条直线附近，则样本数据符合正态分布。而且该直线的斜率为标准差，截距为均值。

**P-P图和Q-Q图的用途基本相同，只是检验方法存在差异。**

**4.小结**

P-P图和Q-Q图可定性判断数据是否符合指定分布，例如正态分布等。值得注意的是，若利用P-P图和Q-Q图判断残差是否符合正态分布，因为原始数据一般没有直接提供残差，所以需先计算出残差，再绘制P-P图和Q-Q图。

2024-08-11 17:57 by admin 25 0

注：本文转载自https://zhuanlan.zhihu.com/p/142628689，如有侵权行为，请联系我们，我们会及时删除。

热门文章